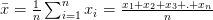ความแตกต่างระหว่างมัธยฐานและเฉลี่ย (เฉลี่ย)

มัธยฐานและค่าเฉลี่ย (เฉลี่ย)

มัธยฐานและค่าเฉลี่ยคือค่ากลางของแนวโน้มในสถิติเชิงพรรณา ค่าเฉลี่ยเลขคณิตมักจะถือเป็นค่าเฉลี่ยของชุดของข้อสังเกต ดังนั้นที่นี่หมายถึงถือว่าเป็นค่าเฉลี่ย อย่างไรก็ตามค่าเฉลี่ยไม่ใช่ค่าเฉลี่ยเลขคณิตตลอดเวลา

เฉลี่ย

ค่าเฉลี่ยเลขคณิตคือผลรวมของค่าข้อมูลหารด้วยจำนวนค่าข้อมูล i. อี

ถ้าข้อมูลมาจากพื้นที่ตัวอย่างเรียกว่าตัวอย่างค่าเฉลี่ย (

) ซึ่งเป็นสถิติเชิงพรรณนาของกลุ่มตัวอย่าง แม้ว่าจะเป็นมาตรการอธิบายที่ใช้โดยทั่วไปสำหรับกลุ่มตัวอย่าง แต่ก็ไม่ใช่สถิติที่มีประสิทธิภาพ มีความไวต่อค่าผิดปกติและการแกว่ง

ตัวอย่างเช่นพิจารณารายได้เฉลี่ยของพลเมืองของเมืองหนึ่ง ๆ เนื่องจากค่าข้อมูลทั้งหมดถูกสรุปและหารด้วยรายได้ของบุคคลที่มั่งคั่งมากจะมีผลต่อค่าเฉลี่ยอย่างมีนัยสำคัญ ดังนั้นค่าเฉลี่ยจึงไม่แสดงถึงข้อมูลที่ดีเสมอไป

นอกจากนี้ในกรณีของสัญญาณสลับกระแสที่ไหลผ่านองค์ประกอบจะแตกต่างกันเป็นระยะ ๆ จากทิศทางบวกไปยังทิศทางลบและในทางกลับกัน ถ้าเราใช้ค่าเฉลี่ยกระแสผ่านองค์ประกอบในช่วงเวลาเดียวจะให้ค่าเป็น 0 ซึ่งหมายความว่าไม่มีกระแสผ่านองค์ประกอบซึ่งชัดไม่เป็นความจริง ดังนั้นในกรณีนี้ค่าเฉลี่ยเลขคณิตไม่ได้เป็นตัววัดที่ดี

ค่าเฉลี่ยเลขคณิตเป็นตัวบ่งชี้ที่ดีเมื่อข้อมูลมีการกระจายอย่างสม่ำเสมอ สำหรับการกระจายแบบปกติค่าเฉลี่ยจะเท่ากับโหมดและค่ามัธยฐาน นอกจากนี้ยังมีส่วนที่เหลือต่ำที่สุดเมื่อพิจารณาถึงข้อผิดพลาดของความคลาดเคลื่อนรากเฉลี่ย ดังนั้นมาตรการที่ดีที่สุดในการอธิบายเมื่อต้องระบุชุดข้อมูลโดยใช้หมายเลขเดียว

มัธยฐาน

ค่าของจุดข้อมูลกลางหลังจัดเรียงข้อมูลทั้งหมดในลำดับที่สูงขึ้นจะถูกกำหนดเป็นค่ามัธยฐานของชุดข้อมูล

•ถ้าจำนวนการสังเกต (จุดข้อมูล) เป็นเลขคี่แล้วมัธยฐานคือการสังเกตตรงกลางของรายการสั่ง

•ถ้าจำนวนการสังเกต (จุดข้อมูล) มีค่าเท่ากับมัธยฐานคือค่าเฉลี่ยของการสังเกตการณ์กลางสองรายการในรายการที่สั่ง

มัธยฐานแบ่งการสังเกตออกเป็นสองกลุ่ม ผม. อี กลุ่ม (50%) ของค่าที่สูงกว่าและกลุ่ม (50%) ของค่าต่ำกว่าค่ามัธยฐาน Median ถูกใช้เฉพาะในการแจกแจงแบบเอียงและแสดงข้อมูลได้ดีกว่าค่าเฉลี่ยเลขคณิต

มัธยฐานเทียบกับค่าเฉลี่ย (เฉลี่ย)

•ค่าเฉลี่ยและมัธยฐานคือค่ากลางของแนวโน้มและสรุปข้อมูล ค่าเฉลี่ยจะไม่ขึ้นกับตำแหน่งของจุดข้อมูล แต่ค่ามัธยฐานจะคำนวณโดยใช้ตำแหน่ง

•ค่าเฉลี่ยมีผลกระทบอย่างมากจากค่าผิดปกติในขณะที่ค่ามัธยฐานไม่ได้รับผลกระทบ

•ค่ามัธยฐานเป็นค่าที่ดีกว่าค่าเฉลี่ยในกรณีของการแจกแจงแบบเบ้สูง

•ในการแจกแจงแบบปกติค่าเฉลี่ยและค่ามัธยฐานจะเหมือนกัน