ความแตกต่างระหว่าง Integrals แน่นอนและไม่แน่นอน ความแตกต่างระหว่าง
แคลคูลัสเป็นสาขาที่สำคัญของคณิตศาสตร์และความแตกต่างมีบทบาทสำคัญในแคลคูลัส กระบวนการผกผันของความแตกต่างที่เรียกว่าบูรณาการและผกผันเป็นที่รู้จักกันเป็นหนึ่งหรือใส่เพียงผกผันของความแตกต่างให้เป็นส่วนประกอบ ขึ้นอยู่กับผลที่พวกเขาผลิต integrals แบ่งออกเป็นสองชั้นคือ integrals แน่นอนและไม่ จำกัด
Definite Integral
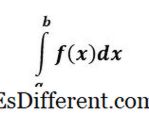
f (x) คือจำนวนเต็มและแสดงพื้นที่ใต้เส้นโค้ง f (x) จาก x = a ไปที่ x = b ปริพันธ์ที่แน่นอนมีข้อ จำกัด ด้านบนและด้านล่างของ integals และเรียกได้ว่าเป็นที่แน่ชัดเนื่องจากในตอนท้ายของปัญหาเรามีตัวเลขเป็นคำตอบที่แน่ชัด
ไม่แน่นอนของ f (x) เป็นฟังก์ชันและตอบคำถามว่า "ฟังก์ชันอะไรที่แตกต่างให้
f (x)? "

ด้วยอินทิกรัลไม่มีที่สิ้นสุดไม่มีข้อ จำกัด ด้านบนและด้านล่างของอินทิเกรตที่นี่และสิ่งที่เราจะได้รับคือคำตอบที่ยังมี x อยู่ในนั้นและจะมีค่าคงที่ (มักแสดงด้วย
C ) ในนั้น
F
นำไปสู่ฟังก์ชันอื่น
f และการรวมกันของ f ให้ค่าคงที่ สัญลักษณ์นี้เขียนเป็น F (x) = ∫ƒ (x) dx หรือ F = ∫ƒ dx
ที่ทั้ง
F
และ
ƒ < เป็นหน้าที่ของ x และ F มีความแตกต่างกัน ในรูปแบบข้างต้นเรียกว่าสมการ Reimann และฟังก์ชันที่เกิดขึ้นมาพร้อมกับค่าคงที่โดยพลการ อินทิกรัลไม่มีที่สิ้นสุดมักสร้างตระกูลของฟังก์ชัน ดังนั้นอินทิกรัลไม่มีที่สิ้นสุด Integrals และกระบวนการบูรณาการเป็นหัวใจของการแก้สมการเชิงอนุพันธ์ อย่างไรก็ตามขั้นตอนในการผสานรวมไม่ได้ทำตามขั้นตอนที่ชัดเจนและเป็นมาตรฐานเสมอไป บางครั้งเราจะเห็นว่าการแก้ปัญหาไม่สามารถแสดงได้อย่างชัดเจนในแง่ของฟังก์ชันพื้นฐาน ในกรณีนี้การแก้ปัญหาการวิเคราะห์มักจะได้รับในรูปของอินทิกรัลไม่ จำกัด ทฤษฎีบทมูลฐานของแคลคูลัส ทฤษฎีบทมูลฐานและแคลคูลัสที่ไม่แน่นอนจะเชื่อมโยงกันโดยทฤษฎีบทมูลฐานของแคลคูลัสดังต่อไปนี้: ในการคำนวณ
ครบถ้วนแน่นอน
หา
ครบถ้วนไม่แน่นอน > (เรียกอีกอย่างว่า anti-derivative) ของฟังก์ชันและประเมินที่จุดสิ้นสุด
x = a และ x = b ความแตกต่างระหว่าง integrals แน่นอนและไม่แน่นอนจะเห็นได้ชัดเมื่อเราประเมิน integrals สำหรับฟังก์ชันเดียวกัน พิจารณาส่วนประกอบต่อไปนี้: ตกลง ลองทำทั้งสองอย่างและดูความแตกต่าง สำหรับการรวมเข้าด้วยกันเราจำเป็นต้องเพิ่มดัชนีลงในดัชนีซึ่งจะนำเราไปสู่นิพจน์ต่อไปนี้: ณ เวลานี้
C
เป็นเพียงค่าคงที่สำหรับเราเท่านั้น ต้องการข้อมูลเพิ่มเติมในปัญหาเพื่อกำหนดค่าที่แม่นยำ

C
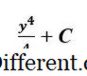
ให้เราประเมินปริพันธ์เดียวกันในรูปแบบที่แน่นอน i. อี โดยมีขีด จำกัด บนและล่างรวมอยู่ด้วย ขณะนี้เรากำลังคำนวณพื้นที่ใต้เส้นโค้ง f (x) = y 3 ระหว่าง
y = 2

และ y = 3 > ขั้นตอนแรกในการประเมินนี้เหมือนกับการประเมินแบบครบวงจรแบบไม่ จำกัด ข้อแตกต่างเพียงอย่างเดียวคือเวลานี้เราไม่ได้เพิ่มค่าคงที่ C การแสดงออกในกรณีนี้มีลักษณะดังนี้: นี่คือการเปิดนำไปสู่: โดยพื้นฐานแล้วเราแทน 3 แล้ว 2 ในนิพจน์และได้รับความแตกต่างระหว่างพวกเขา
นี่คือค่าที่แน่นอนเมื่อเทียบกับการใช้ค่าคงที่ C ก่อนหน้านี้
ลองดูปัจจัยคงที่ (เกี่ยวกับอินทิกรัลไม่ จำกัด) ในรายละเอียดเพิ่มเติม

หากความแตกต่างของ

y
3 คือ 3y
2
จากนั้น 3y 2 dy = y 3 อย่างไรก็ตาม 3y
2 อาจเป็นความแตกต่างของการแสดงออกหลายอย่างซึ่งรวมถึง y 3 -5 , > y 3 +7 ฯลฯ ซึ่งหมายความว่าการกลับรายการจะไม่ซ้ำกันเนื่องจากค่าคงที่จะไม่ได้รับการระบุไว้ในระหว่างการดำเนินการ โดยทั่วไป 3y 2 คือความแตกต่างของ y 3 + C ที่
C เป็นค่าคงที่ใด ๆ อนึ่ง C เรียกว่า 'ค่าคงที่ของการรวมกลุ่ม' เราเขียนว่า: ∫ 3y 2 dx = y 3 + C
เทคนิคการรวมสำหรับอินทิกรัลไม่ จำกัด เช่นการค้นหาตารางหรือการรวม Risch สามารถเพิ่มความไม่ต่อเนื่องใหม่ระหว่างกระบวนการรวมกันได้ ความไม่ต่อเนื่องใหม่เหล่านี้ปรากฏขึ้นเนื่องจากอนุพันธ์แอนตี้บลูทู ธ สามารถนำมาใช้ลอการิทึมที่ซับซ้อนได้
ลอการิทึมที่ซับซ้อนมีความไม่ต่อเนื่องในการกระโดดเมื่ออาร์กิวเมนต์ตัดผ่านแกนจริงเชิงลบและอัลกอริทึมการรวมกันบางครั้งไม่สามารถหาการแทนซึ่งการยกเลิกเหล่านี้จะยกเลิก ถ้าปริพันธ์ที่แน่นอนได้รับการประเมินด้วยการคำนวณอินทิกรัลอย่างไม่ จำกัด ก่อนและจากนั้นใช้ขอบเขตการรวมเข้ากับผลลัพธ์เราต้องทราบว่าการรวมกันแบบไม่แน่นอนอาจทำให้เกิดความไม่ต่อเนื่อง ถ้าเป็นเช่นนี้เราต้องตรวจสอบความไม่ต่อเนื่องในช่วงการรวมกิจการ



