ความแตกต่างระหว่าง Derivative and Differential

อนุพันธ์และความแตกต่าง

ในแคลคูลัสเชิงอนุพันธ์อนุพันธ์และความแตกต่างของฟังก์ชันมีความสัมพันธ์กัน แต่มีความหมายที่แตกต่างกันมาก ใช้เพื่อแสดงสองวัตถุทางคณิตศาสตร์ที่สำคัญที่เกี่ยวข้องกับการทำงาน differentiable

อนุพันธ์คืออะไร?

อนุพันธ์ของฟังก์ชันจะวัดอัตราที่ค่าฟังก์ชันจะเปลี่ยนแปลงตามการเปลี่ยนแปลงของอินพุต ในฟังก์ชันหลายตัวแปรการเปลี่ยนแปลงค่าฟังก์ชันขึ้นอยู่กับทิศทางของการเปลี่ยนแปลงค่าของตัวแปรอิสระ ดังนั้นในกรณีดังกล่าวจะมีการเลือกทิศทางที่เฉพาะเจาะจงและหน้าที่แตกต่างกันไปในทิศทางนั้น อนุพันธ์ดังกล่าวเรียกว่าอนุพันธ์เชิงทิศทาง อนุพันธ์บางส่วนเป็นอนุพันธ์ทางการเงินแบบพิเศษ

-1->

อนุพันธ์ของฟังก์ชันที่มีค่าเวกเตอร์ f สามารถกำหนดเป็นขีด จำกัด

ได้ทุกที่ที่มีอยู่ ดังที่ได้กล่าวมาก่อนหน้านี้ทำให้เรามีอัตราการเพิ่มขึ้นของฟังก์ชัน f ไปตามทิศทางของเวกเตอร์ u ในกรณีของฟังก์ชันที่มีค่าเดียวค่านี้จะลดลงตามคำจำกัดความที่รู้จักกันดีของอนุพันธ์

ตัวอย่างเช่น

มีความแตกต่างกันไปทุกหนทุกแห่งและอนุพันธ์มีค่าเท่ากับขีด จำกัด

ซึ่งเท่ากับ

อนุพันธ์ของฟังก์ชันเช่น

มีอยู่ทุกหนทุกแห่ง มีความสัมพันธ์กับฟังก์ชัน

ตามลำดับ

นี่เรียกว่าอนุพันธ์อันดับแรก โดยปกติอนุพันธ์แรกของฟังก์ชัน

f แสดงด้วย f (1) ^{ตอนนี้ใช้สัญกรณ์นี้คุณสามารถกำหนดอนุพันธ์ที่มีลำดับขั้นสูงได้} เป็นอนุพันธ์ทิศทางลำดับที่สองและแสดงถึงอนุพันธ์

n th ^โดย f ( ^{n) สำหรับแต่ละ} n, กำหนด

n th ^{อนุพันธ์} ความแตกต่างคืออะไร?

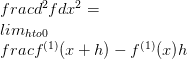
ความแตกต่างของฟังก์ชันแสดงถึงการเปลี่ยนแปลงของฟังก์ชันเกี่ยวกับการเปลี่ยนแปลงตัวแปรอิสระหรือตัวแปร ในสัญกรณ์ตามปกติสำหรับฟังก์ชันที่กำหนด

f ของตัวแปรเดี่ยว x ความแตกต่างทั้งหมดของลำดับที่ 1 df คือ ให้โดย ซึ่งหมายความว่าสำหรับการเปลี่ยนแปลงที่น้อยที่สุด

x (เช่น d x) จะมี f (1) ⁽ x <) d x เปลี่ยน f. การใช้ข้อ จำกัด สามารถสรุปคำจำกัดความนี้ได้ดังนี้ สมมติว่าΔ x

คือการเปลี่ยนแปลง x ที่จุดใด ๆ x และ f คือการเปลี่ยนแปลงที่ตรงกันในฟังก์ชัน ฉ สามารถแสดงให้เห็นว่าΔ f = f (1) ( ^x ) Δ x + ε, โดยที่εคือ ข้อผิดพลาด. ตอนนี้ขีด จำกัด Δ x → x ⁼ (1) ( _{x) (โดยใช้คำจำกัดความของอนุพันธ์ที่ระบุไว้ก่อนหน้านี้) และด้วยเหตุนี้} x <> ^/ x = 0ดังนั้นจึงเป็นไปได้ที่จะสรุปได้ว่าΔ x → 0 ε ^{= 0. ขณะนี้แสดงว่า} x → _{0 Δ f} d f และ x → 0 Δ x เป็น d x การกำหนดความแตกต่างได้รับอย่างจริงจัง ตัวอย่างเช่นความแตกต่างของฟังก์ชัน คือ ในกรณีของฟังก์ชันของตัวแปรสองตัวหรือมากกว่านั้นความแตกต่างทั้งหมดของฟังก์ชันจะถูกกำหนดเป็นผลรวมของความแตกต่างในทิศทางของตัวแปรแต่ละตัว ในทางคณิตศาสตร์ก็สามารถระบุเป็น อะไรคือความแตกต่างระหว่าง derivative และ differential? •อนุพันธ์หมายถึงอัตราการเปลี่ยนแปลงของฟังก์ชันในขณะที่ความแตกต่างหมายถึงการเปลี่ยนแปลงที่แท้จริงของฟังก์ชันเมื่อตัวแปรอิสระมีการเปลี่ยนแปลง อนุพันธ์มาจาก แต่ความแตกต่างจะได้รับจาก