ความแตกต่างระหว่างความแตกต่างและอนุพันธ์

การแตกต่างและอนุพันธ์

ในแคลคูลัสเชิงอนุพันธ์อนุพันธ์และความแตกต่างมีความสัมพันธ์กันอย่างใกล้ชิด แต่แตกต่างกันมากและใช้เพื่อแสดงถึงความสำคัญสองทางคณิตศาสตร์ แนวคิดเกี่ยวกับการทำงาน

อนุพันธ์คืออะไร?

อนุพันธ์ของฟังก์ชันจะวัดอัตราที่ค่าฟังก์ชันจะเปลี่ยนแปลงตามการเปลี่ยนแปลงของอินพุต ในฟังก์ชันหลายตัวแปรการเปลี่ยนแปลงค่าฟังก์ชันขึ้นอยู่กับทิศทางของการเปลี่ยนแปลงค่าของตัวแปรอิสระ ดังนั้นในกรณีดังกล่าวจะมีการเลือกทิศทางที่เฉพาะเจาะจงและหน้าที่แตกต่างกันไปในทิศทางนั้น อนุพันธ์ดังกล่าวเรียกว่าอนุพันธ์เชิงทิศทาง อนุพันธ์บางส่วนเป็นอนุพันธ์ทางการเงินแบบพิเศษ

-1->

อนุพันธ์ของฟังก์ชันที่มีค่าเวกเตอร์ f สามารถกำหนดเป็นขีด จำกัด

ได้ทุกที่ที่มีอยู่ ดังที่ได้กล่าวมาก่อนหน้านี้ทำให้เรามีอัตราการเพิ่มขึ้นของฟังก์ชัน f ไปตามทิศทางของเวกเตอร์ u ในกรณีของฟังก์ชันที่มีค่าเดียวค่านี้จะลดลงตามคำจำกัดความที่รู้จักกันดีของอนุพันธ์

ตัวอย่างเช่น

มีความแตกต่างกันไปทุกหนทุกแห่งและอนุพันธ์มีค่าเท่ากับขีด จำกัด

ซึ่งเท่ากับ

อนุพันธ์ของฟังก์ชันเช่น

มีอยู่ทุกหนทุกแห่ง มีความสัมพันธ์กับฟังก์ชัน

ตามลำดับ

นี่เรียกว่าอนุพันธ์อันดับแรก โดยปกติอนุพันธ์แรกของฟังก์ชัน

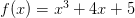
f แสดงด้วย f (1) ^{ตอนนี้ใช้สัญกรณ์นี้คุณสามารถกำหนดอนุพันธ์ที่มีลำดับขั้นสูงได้} เป็นอนุพันธ์ทิศทางลำดับที่สองและแสดงถึงอนุพันธ์

n th ^โดย f ( ^{n) สำหรับแต่ละ} n, กำหนด

n th ^{อนุพันธ์} ความแตกต่างคืออะไร?

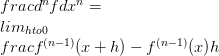
ความแตกต่างคือกระบวนการหาอนุพันธ์ของฟังก์ชัน differentiable D- ดำเนินการแสดงโดย

D แสดงความแตกต่างในบางบริบท ถ้า x เป็นตัวแปรอิสระแล้ว D d ^/ dx _{ตัวดำเนินการ D เป็นโอเปอเรเตอร์เชิงเส้น i. อี สำหรับสมการสองตัวที่แตกต่างกัน} f และ g และคงที่ c, คุณสมบัติต่อไปนี้ ฉัน

D (f + g) = D (f) + D (g) II

D (cf) = cD (f) การใช้ D-operator, กฎอื่น ๆ ที่เกี่ยวข้องกับความแตกต่างสามารถแสดงได้ดังนี้.

D (f g) = D (f) g + f D (999) D (f / ^g ) = D ^{(f (f f (g)) /} o _g ^{) = (} D (f) o g) D (g) ตัวอย่างเช่นเมื่อ F (x) = x 2 บาป x

จะแตกต่างกับ x โดยใช้ กฎที่ระบุให้คำตอบคือ 2 x ^บาป x - + x 2 cos x อะไรคือความแตกต่างระหว่างความแตกต่างและอนุพันธ์? • Derivative หมายถึงอัตราการเปลี่ยนแปลงของฟังก์ชัน •ความแตกต่างคือกระบวนการหาอนุพันธ์ของฟังก์ชัน