ความแตกต่างระหว่างรูปสี่เหลี่ยมด้านขนานและรูปสี่เหลี่ยมคางหมู: รูปสี่เหลี่ยมขนมเปียกปูนกับรูปสี่เหลี่ยมผืนผ้า

รูปสี่เหลี่ยมด้านขั้วกับรูปสี่เหลี่ยมจัตุรัส < รูปสี่เหลี่ยมและรูปสี่เหลี่ยมขนมเปียกปิ่งเป็นรูปหลายเหลี่ยมที่พบในเรขาคณิตยุคลิด รูปสี่เหลี่ยมด้านขนานเป็นกรณีพิเศษของรูปสี่เหลี่ยมขนมเปียกปูน สี่เหลี่ยมจัตุรัสสามารถเป็นได้ทั้งแบบระนาบ (2D) หรือ 3 มิติในขณะที่รูปสี่เหลี่ยมขนมเปียกป์เป็นแนวระนาบ

รูปสี่เหลี่ยมผืนผ้า

รูปสี่เหลี่ยมคางหมูเป็นรูปหลายเหลี่ยมที่มีสี่ด้าน มีจุดยอดรวม 4 จุดและมุมภายในเป็น 3600 (2π rad) รูปสี่เหลี่ยมขนมเปียกปูนถูกแบ่งออกเป็นรูปสี่เหลี่ยมขนมเปียกปูนแบบตัดตัวเอง สี่เหลี่ยมจัตุรัสที่ตัดกันด้วยตัวเองมีสองด้านหรือมากกว่าที่ข้ามกันและกันและรูปทรงเรขาคณิตที่มีขนาดเล็ก (เช่นรูปสามเหลี่ยมจะมีรูปสี่เหลี่ยมผืนผ้า)

รูปสี่เหลี่ยมจัตุรัสที่เรียบง่ายแบ่งออกเป็นรูปสี่เหลี่ยมขนมนุมและเว้า รูปสี่เหลี่ยมเวี้ยวเว้ามีด้านที่อยู่ติดกันสร้างมุมสะท้อนภายในรูป รูปสี่เหลี่ยมผืนผ้าที่เรียบง่ายซึ่งไม่มีมุมสะท้อนอยู่ภายในเป็นรูปสี่เหลี่ยมขนมนอบ รูปสี่เหลี่ยมจัตุรัสนูนสามารถมี tessellations ได้เสมอ

ส่วนสำคัญของรูปเรขาคณิตของรูปสี่เหลี่ยมในระดับเริ่มต้นจะเกี่ยวข้องกับรูปสี่เหลี่ยมขนมนูน บางรูปสี่เหลี่ยมผืนผ้ามีความคุ้นเคยกับเรามากจากวันที่โรงเรียนประถมศึกษา ต่อไปนี้เป็นแผนภาพที่แสดงรูปสี่เหลี่ยมขนมนั่วที่แตกต่างกัน

รูปสี่เหลี่ยมด้านขนาน

รูปสี่เหลี่ยมด้านขนานสามารถกำหนดเป็นรูปทรงเรขาคณิตที่มีสี่ด้านโดยมีด้านตรงข้ามขนานกัน แม่นยำมากขึ้นเป็นรูปสี่เหลี่ยมขนมเปียกปูนที่มีสองด้านคู่ขนาน ลักษณะขนานนี้ให้ลักษณะทางเรขาคณิตมากกับรูปสี่เหลี่ยมขนมเปียกปูน

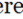
รูปสี่เหลี่ยมคางขนานเป็นรูปสี่เหลี่ยมด้านขนานหากพบลักษณะทางเรขาคณิตต่อไปนี้

•คู่ของฝ่ายตรงข้ามสองคู่มีความยาวเท่ากัน (AB = DC, AD = BC)

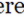
•สองมุมคู่ต่อสู้มีขนาดเท่ากัน ()

•ถ้ามุมที่อยู่ติดกันเสริม

•คู่ข้างซึ่งเป็นฝ่ายตรงข้ามกันมีขนานและมีความยาวเท่ากับ (AO = OC, BO = OD)

•แต่ละเส้นทแยงมุมจะแบ่งรูปสี่เหลี่ยมผืนผ้าออกเป็นสองเหลี่ยมผืนผ้าที่เหมือนกันสองแฉก (AB = DC และAB∥DC)

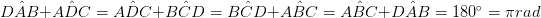
(ΔADB≡ΔBCD, ΔABC≡ΔADC)

นอกจากนี้ผลรวมของสี่เหลี่ยมของด้านข้างจะเท่ากับผลรวมของสี่เหลี่ยมของเส้นทแยงมุม นี่คือบางครั้งเรียกว่ากฎหมายพิกเซลทางปริยาย

และมีการใช้งานทางฟิสิกส์และวิศวกรรมอย่างกว้างขวาง (AB

2 + BC 2 ^{+ CD} 2 ^{+ DA} 2 ^{= AC} 2 ^{+ BD} 2 ⁾ แต่ละลักษณะข้างต้นสามารถใช้เป็นสมบัติได้เมื่อมีการจัดตั้งว่ารูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมขนมเปียกปูน ^{พื้นที่ของรูปสี่เหลี่ยมด้านขนานสามารถคำนวณได้จากผลิตภัณฑ์ที่มีความยาวของด้านใดด้านหนึ่งและด้านสูงตรงข้ามกับด้านใดด้านหนึ่ง ดังนั้นพื้นที่ของรูปสี่เหลี่ยมด้านขนานสามารถระบุได้เป็น} พื้นที่ของรูปสี่เหลี่ยมด้านขั้ว = ฐาน×สูง =

AB

×

h พื้นที่ของรูปสี่เหลี่ยมด้านขนานนั้นไม่ขึ้นอยู่กับรูปร่างของรูปสี่เหลี่ยมขนมเปี้ยน ขึ้นอยู่กับความยาวฐานและความสูงตั้งฉากเท่านั้น หากด้านของรูปสี่เหลี่ยมด้านขนานสามารถแสดงได้ด้วยสองเวกเตอร์พื้นที่สามารถหาได้จากขนาดของผลิตภัณฑ์เวกเตอร์ (ผลิตภัณฑ์ข้าม) ของสองพาหะที่อยู่ติดกัน ถ้าด้าน AB และ AD แสดงด้วยเวกเตอร์ (

) และ () ตามลำดับพื้นที่ของรูปสี่เหลี่ยมด้านขั้วจะได้รับโดย

โดยที่αคือมุมระหว่าง

ถึง

ต่อไปนี้เป็นคุณสมบัติขั้นสูงของรูปสี่เหลี่ยมด้านขนาน

•พื้นที่สี่เหลี่ยมด้านขนานเป็นสองเท่าของพื้นที่สามเหลี่ยมที่สร้างโดยเส้นทแยงมุมใด ๆ

•พื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนแบ่งครึ่งโดยเส้นผ่านจุดกึ่งกลาง

•การแปลงเลียนแบบที่ไม่ใช่ความเสื่อมที่เกิดขึ้นจะมีรูปสี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเป้นอื่น ๆ

•รูปสี่เหลี่ยมด้านขนานมีสมมาตรหมุนตามลำดับ 2

•ระยะทางจากจุดภายในของรูปสี่เหลี่ยมด้านขนานไปยังด้านต่างๆ ตำแหน่งของจุด

ความแตกต่างระหว่างรูปสี่เหลี่ยมด้านขนานกับสี่เหลี่ยมเท่าไร?

รูปสี่เหลี่ยมผืนผ้าเป็นรูปหลายเหลี่ยมที่มีสี่ด้าน (บางครั้งเรียกว่า tetragons) ในขณะที่รูปสี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเปียกปูนแบบพิเศษ

รูปสี่เหลี่ยมผืนผ้าสามารถมีด้านข้างของเครื่องบินต่างๆ (ในพื้นที่ 3 มิติ) ในขณะที่ด้านข้างของรูปสี่เหลี่ยมขนมเปียกปูนอยู่บนระนาบเดียวกัน (ระนาบ / 2 มิติ)

•มุมภายในของรูปสี่เหลี่ยมขนมขอบสามารถใช้ค่าใด ๆ (รวมถึงมุมสะท้อน) เพื่อให้มีความสูงได้ถึง 3600 พิกเซลสามารถมีมุมเท่าเป็นมุมสูงสุดเท่านั้น

•สี่ด้านของรูปสี่เหลี่ยมขนมเปียกปูนสามารถมีความยาวต่างกันในขณะที่ด้านตรงข้ามของรูปสี่เหลี่ยมด้านขนานขนานกันและมีความยาวเท่ากัน

•เส้นทแยงมุมใด ๆ แบ่งรูปสี่เหลี่ยมด้านขนานออกเป็นสองรูปสามเหลี่ยมที่เท่ากันในขณะที่รูปสามเหลี่ยมที่มีเส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูนทั่วไปไม่จำเป็นต้องสอดคล้องกัน