ความแตกต่างระหว่าง Parallelogram และ Rhombus: รูปขนานกับ Rhombus
รูปขนานกับแรด
รูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมขนมเปียกปูน รูปเรขาคณิตของตัวเลขเหล่านี้เป็นที่รู้จักของมนุษย์เป็นเวลาหลายพันปี เรื่องนี้ได้รับการกล่าวไว้อย่างชัดเจนในหนังสือ "Elements" ที่เขียนขึ้นโดยนักคณิตศาสตร์กรีก Euclid
รูปสี่เหลี่ยมด้านขนาน
รูปสี่เหลี่ยมด้านขนานสามารถกำหนดเป็นรูปทรงเรขาคณิตสี่ด้านโดยมีด้านตรงข้ามขนานกัน แม่นยำมากขึ้นเป็นรูปสี่เหลี่ยมขนมเปียกปูนมีสองด้านคู่ขนาน ลักษณะขนานนี้ให้ลักษณะทางเรขาคณิตมากกับรูปสี่เหลี่ยมขนมเปียกปูน

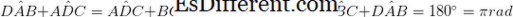
รูปสี่เหลี่ยมคางขนานเป็นรูปสี่เหลี่ยมด้านขนานหากพบลักษณะทางเรขาคณิตต่อไปนี้
•คู่ของฝ่ายตรงข้ามสองคู่มีความยาวเท่ากัน (AB = DC, AD = BC)
•สองมุมคู่ต่อสู้มีขนาดเท่ากัน (
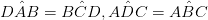
•คู่ข้างซึ่งเป็นฝ่ายตรงข้ามกันมีขนานและมีความยาวเท่ากัน (AB = DC และAB∥DC)
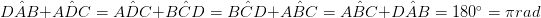
(AO = OC, BO = OD)
•แต่ละเส้นทแยงมุมจะแบ่งรูปสี่เหลี่ยมขนมขอบออกเป็นสองแฉกที่เหมือนกัน (ΔADB≡ΔBCD, ΔABC≡ΔADC)นอกจากนี้ผลรวมของสี่เหลี่ยมของด้านข้างจะเท่ากับผลรวมของสี่เหลี่ยมของเส้นทแยงมุม นี่คือบางครั้งเรียกว่ากฎหมายพิกเซลทางปริยาย
และมีการใช้งานทางฟิสิกส์และวิศวกรรมอย่างกว้างขวาง (AB
2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2 ) แต่ละลักษณะข้างต้นสามารถใช้เป็นสมบัติได้เมื่อมีการจัดตั้งว่ารูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมขนมเปียกปูน พื้นที่ของรูปสี่เหลี่ยมด้านขนานสามารถคำนวณได้จากผลิตภัณฑ์ที่มีความยาวของด้านใดด้านหนึ่งและด้านสูงตรงข้ามกับด้านใดด้านหนึ่ง ดังนั้นพื้นที่ของรูปสี่เหลี่ยมด้านขนานสามารถระบุได้เป็น พื้นที่ของรูปสี่เหลี่ยมด้านขั้ว = ฐาน×สูง = AB × h
พื้นที่ของรูปสี่เหลี่ยมขนาดเป็นอิสระจากรูปทรงสี่เหลี่ยมลูกบาศก์แต่ละ ขึ้นอยู่กับความยาวฐานและความสูงตั้งฉากเท่านั้น
หากด้านของรูปสี่เหลี่ยมด้านขนานสามารถแสดงได้ด้วยสองเวกเตอร์พื้นที่สามารถหาได้จากขนาดของผลิตภัณฑ์เวกเตอร์ (ผลิตภัณฑ์ข้าม) ของสองพาหะที่อยู่ติดกัน
ถ้าด้าน AB และ AD แสดงด้วยเวกเตอร์ (
 ) และ () ตามลำดับพื้นที่ของรูปสี่เหลี่ยมด้านขั้วจะได้รับโดย
) และ () ตามลำดับพื้นที่ของรูปสี่เหลี่ยมด้านขั้วจะได้รับโดย
โดยที่αคือมุมระหว่าง





•รูปสี่เหลี่ยมด้านขนานมีสมมาตรหมุนตามลำดับ 2
•ระยะทางจากจุดภายในของรูปสี่เหลี่ยมด้านขนานไปยังด้านต่างๆ ตำแหน่งของจุด
Rhombus
รูปสี่เหลี่ยมขนมเปียกปูนกับทุกด้านมีความยาวเท่ากันเป็นที่รู้จักกันว่าเป็นรูปสี่เหลี่ยมขนมเปียกปูน นอกจากนี้ยังมีชื่อว่า
รูปสี่เหลี่ยมด้านขนาน ถือเป็นรูปเพชรที่คล้ายกับเพชรที่เล่น
Rhombus เป็นกรณีพิเศษของรูปสี่เหลี่ยมขนมเปียกปูน ถือได้ว่าเป็นสี่เหลี่ยมด้านขนานที่มีทั้งสี่ด้านเท่ากัน และมีคุณสมบัติพิเศษนอกเหนือจากคุณสมบัติของรูปสี่เหลี่ยมขนมเปียกปูน
•เส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูนแบ่งกันที่มุมขวา เส้นทแยงมุมอยู่ในแนวตั้ง
•ทแยงมุมแบ่งมุมทั้งสองด้านออก •อย่างน้อยสองด้านที่ติดกันมีความยาวเท่ากัน พื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนสามารถคำนวณได้ด้วยวิธีเดียวกันกับรูปสี่เหลี่ยมด้านขนาน


ความแตกต่างระหว่าง Parallelogram และ Rhombus คืออะไร?
•รูปสี่เหลี่ยมด้านขนานและรูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมผืนผ้า Rhombus เป็นกรณีพิเศษของรูปสี่เหลี่ยมขนมเปียกปูน
•พื้นที่ใด ๆ ที่สามารถคำนวณได้โดยใช้ฐานสูตร x height
•พิจารณาเส้นทแยงมุม
- เส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนานแยกออกเป็นสองส่วนและแบ่งรูปสี่เหลี่ยมด้านขนานออกเป็นรูปสามเหลี่ยมที่เท่ากัน
- เส้นทแยงมุมของรูปสี่เหลี่ยมขนมเปียกปูนแบ่งกันที่มุมขวาและรูปสามเหลี่ยมที่มีรูปด้านเท่ากัน
•พิจารณามุมภายใน
- การคัดค้านมุมภายในของรูปสี่เหลี่ยมด้านขนานมีขนาดเท่ากัน มีมุมเสริมภายในสองมุม
- มุมภายในของรูปสี่เหลี่ยมขนมเปียกปูนแบ่งตามแนวทแยงมุม
•พิจารณาด้านข้าง
- ในรูปสี่เหลี่ยมด้านขนาน, ผลรวมของสี่เหลี่ยมของด้านข้างเท่ากับผลรวมของสี่เหลี่ยมของเส้นทแยงมุม (กฎหมายแนวขนาน)
- เมื่อทั้งสี่ด้านมีขนาดเท่ากันในรูปสี่เหลี่ยมจัตุรัสสี่เหลี่ยมสี่เหลี่ยมด้านหนึ่งจะเท่ากับผลรวมของสี่เหลี่ยมจัตุรัส




