ความแตกต่างระหว่างรูปสี่เหลี่ยมและรูปสี่เหลี่ยมคางหมู: รูปคู่ขนานกับรูปสี่เหลี่ยมคางหมู (รูปสี่เหลี่ยมคางหมู)

รูปสี่เหลี่ยมด้านขนานและรูปสี่เหลี่ยมคางหมู

รูปสี่เหลี่ยมด้านขนานและรูปสี่เหลี่ยมคางหมู (หรือรูปสี่เหลี่ยมคางหมู) แม้ว่ารูปสี่เหลี่ยมจัตุรัสเหล่านี้เป็นรูปสี่เหลี่ยมรูปทรงเรขาคณิตของรูปสี่เหลี่ยมคางหมูแตกต่างจากรูปสี่เหลี่ยมขนมเปียกปูน

รูปสี่เหลี่ยมด้านขนาน

รูปสี่เหลี่ยมด้านขนานสามารถกำหนดเป็นรูปทรงเรขาคณิตที่มีสี่ด้านโดยมีด้านตรงข้ามขนานกัน แม่นยำมากขึ้นเป็นรูปสี่เหลี่ยมขนมเปียกปูนมีสองด้านคู่ขนาน ลักษณะขนานนี้ให้ลักษณะทางเรขาคณิตมากกับรูปสี่เหลี่ยมขนมเปียกปูน

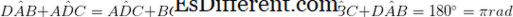
รูปสี่เหลี่ยมคางขนานเป็นรูปสี่เหลี่ยมด้านขนานหากพบลักษณะทางเรขาคณิตต่อไปนี้

•คู่ของฝ่ายตรงข้ามสองคู่มีความยาวเท่ากัน (AB = DC, AD = BC)

•สองมุมคู่ต่อสู้มีขนาดเท่ากัน (

)

ถ้ามุมที่อยู่ติดกันเสริม

•คู่ข้างซึ่งเป็นฝ่ายตรงข้ามกันมีขนานและมีความยาวเท่ากัน (AB = DC และAB∥DC)

(AO = OC, BO = OD)

•แต่ละเส้นทแยงมุมจะแบ่งรูปสี่เหลี่ยมขนมขอบออกเป็นสองแฉกที่เหมือนกัน (ΔADB≡ΔBCD, ΔABC≡ΔADC)

นอกจากนี้ผลรวมของสี่เหลี่ยมของด้านข้างจะเท่ากับผลรวมของสี่เหลี่ยมของเส้นทแยงมุม นี่คือบางครั้งเรียกว่ากฎหมายพิกเซลทางปริยาย

และมีการใช้งานทางฟิสิกส์และวิศวกรรมอย่างกว้างขวาง (AB

2 + BC 2 ^{+ CD} 2 ^{+ DA} 2 ^{= AC} 2 ^{+ BD} 2 ⁾ แต่ละลักษณะข้างต้นสามารถใช้เป็นสมบัติได้เมื่อมีการจัดตั้งว่ารูปสี่เหลี่ยมขนมเปียกปูนเป็นรูปสี่เหลี่ยมขนมเปียกปูน ^{พื้นที่ของรูปสี่เหลี่ยมด้านขนานสามารถคำนวณได้จากผลิตภัณฑ์ที่มีความยาวของด้านใดด้านหนึ่งและด้านสูงตรงข้ามกับด้านใดด้านหนึ่ง ดังนั้นพื้นที่ของรูปสี่เหลี่ยมด้านขนานสามารถระบุได้เป็น} พื้นที่ของรูปสี่เหลี่ยมด้านขั้ว = ฐาน×สูง =

AB

×

h พื้นที่ของรูปสี่เหลี่ยมด้านขนานนั้นไม่ขึ้นอยู่กับรูปร่างของรูปสี่เหลี่ยมขนมเปี้ยน ขึ้นอยู่กับความยาวฐานและความสูงตั้งฉากเท่านั้น หากด้านของรูปสี่เหลี่ยมด้านขนานสามารถแสดงได้ด้วยสองเวกเตอร์พื้นที่สามารถหาได้จากขนาดของผลิตภัณฑ์เวกเตอร์ (ผลิตภัณฑ์ข้าม) ของสองพาหะที่อยู่ติดกัน ถ้าด้าน AB และ AD แสดงด้วยเวกเตอร์ (

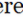) และ () ตามลำดับพื้นที่ของรูปสี่เหลี่ยมด้านขั้วจะได้รับโดย

โดยที่αคือมุมระหว่าง

ถึง

ต่อไปนี้เป็นคุณสมบัติขั้นสูงของรูปสี่เหลี่ยมด้านขนาน

•พื้นที่สี่เหลี่ยมด้านขนานเป็นสองเท่าของพื้นที่สามเหลี่ยมที่สร้างโดยเส้นทแยงมุมใด ๆ

•พื้นที่ของรูปสี่เหลี่ยมขนมเปียกปูนแบ่งครึ่งโดยเส้นผ่านจุดกึ่งกลาง

•การแปลงเลียนแบบที่ไม่ใช่ความเสื่อมที่เกิดขึ้นจะมีรูปสี่เหลี่ยมด้านขนานเป็นรูปสี่เหลี่ยมขนมเป้นอื่น ๆ

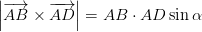
•รูปสี่เหลี่ยมด้านขนานมีสมมาตรหมุนตามลำดับ 2

•ระยะทางจากจุดภายในของรูปสี่เหลี่ยมด้านขนานไปยังด้านต่างๆ ตำแหน่งของจุด

Trapezoid

Trapezoid (หรือ

Trapezium

เป็นภาษาอังกฤษแบบอังกฤษ) เป็นรูปสี่เหลี่ยมขนมเปียกปูนที่มีด้านยาวอย่างน้อยสองด้านขนานและไม่เท่ากัน ด้านคู่ขนานของรูปสี่เหลี่ยมคางหมูเรียกว่าฐานและอีกสองด้านเรียกว่าขา

ต่อไปนี้เป็นลักษณะสำคัญของ trapezoids;

•ถ้ามุมที่อยู่ติดกันไม่ได้อยู่บนฐานเดียวกันกับรูปสี่เหลี่ยมคางหมูจะเป็นมุมเสริม ผม. อี พวกเขาเพิ่มขึ้นได้ถึง 180 ° ( ) •

ทแยงมุมทั้งสองแบบของ trapezium ตัดกันในอัตราส่วนเดียวกัน (อัตราส่วนระหว่างส่วนของเส้นทแยงมุมเท่ากับ)

•

ถ้า a และ b เป็นฐานและ c d คือขาความยาวของเส้นทแยงมุมจะถูกกำหนดด้วย

และ พื้นที่ของรูปสี่เหลี่ยมคางหมูสามารถคำนวณได้โดยใช้สูตรดังต่อไปนี้

พื้นที่ รูปสี่เหลี่ยมคางหมู = ความแตกต่างระหว่างรูปสี่เหลี่ยมด้านขนานกับรูปสี่เหลี่ยมคางหมู (Trapezium) คืออะไร?

•

ทั้งสองรูปสี่เหลี่ยมด้านขนานและรูปสี่เหลี่ยมคางหมูเป็นรูปสี่เหลี่ยมขนมนอบ

•

ในรูปสี่เหลี่ยมด้านขนานทั้งสองฝ่ายของฝ่ายตรงข้ามขนานในขณะที่ในรูปสี่เหลี่ยมคางหมูเพียงคู่ขนาน

• เส้นทแยงมุมของรูปสี่เหลี่ยมด้านขนานวางทับกันและกัน (อัตราส่วน 1: 1) ในขณะที่เส้นทแยงมุมของสี่เหลี่ยมคางหมูตรงกับอัตราส่วนคงที่ระหว่างส่วนต่างๆ

• พื้นที่ของรูปสี่เหลี่ยมขนาดจะขึ้นอยู่กับความสูงและฐานในขณะที่พื้นที่ของสี่เหลี่ยมคางหมูขึ้นอยู่กับความสูงและช่วงกลาง

• รูปสามเหลี่ยมสองรูปที่มีเส้นทแยงมุมรูปสี่เหลี่ยมด้านขนานมีความสอดคล้องกันในขณะที่รูปสามเหลี่ยมของรูปสี่เหลี่ยมคางหมูสามารถเป็นที่ยอมรับได้หรือไม่