ความแตกต่างระหว่าง Power Series กับ Taylor Series
ซีรีส์พาวเวอร์และเทย์เลอร์ซีรีส์
ในคณิตศาสตร์ลำดับจริงคือรายการที่เรียงลำดับของจำนวนจริง. อย่างเป็นทางการเป็นฟังก์ชันจากชุดของจำนวนธรรมชาติในชุดของตัวเลขจริง ถ้า n คือระยะ n th ของลำดับเราแสดงลำดับโดยหรือ 1 , a 2 , …, n, … ตัวอย่างเช่นพิจารณาลำดับที่ 1, ½, ⅓, …, 1 / n , … สามารถแสดงได้ว่า {1 / n}
เป็นไปได้ที่จะกำหนดลำดับโดยใช้ลำดับ ชุดคือผลรวมของเงื่อนไขของลำดับ ดังนั้นสำหรับแต่ละลำดับมีลำดับที่เกี่ยวข้องและในทางกลับกัน ถ้า {a n} เป็นลำดับภายใต้การพิจารณาแล้วชุดที่สร้างขึ้นตามลำดับดังกล่าวสามารถแสดงเป็น:
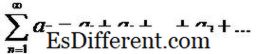
ดังนั้นในตัวอย่างข้างต้นชุดที่เกี่ยวข้องคือ 1 + 1 / 2 + 1 / 3 + … + 1 / n + … ตามที่แนะนำชื่อชุดพลังงานคือชุดข้อมูลพิเศษและใช้ในการวิเคราะห์เชิงตัวเลขและแบบจำลองทางคณิตศาสตร์ที่เกี่ยวข้อง เทย์เลอร์ซีรี่ส์เป็นชุดพลังงานพิเศษที่ให้ทางเลือกและใช้งานง่ายในการแสดงฟังก์ชั่นที่รู้จักกันดี
ชุดพลังงานเป็นชุดรูปแบบ
999 ซึ่งสามารถบรรจบกันได้ (บางช่วง) สำหรับช่วงกึ่งกลางที่
c
ค่าสัมประสิทธิ์ n สามารถเป็นตัวเลขจริงหรือซับซ้อนและไม่ขึ้นกับ x; ผม. อี ตัวแปรดัมมี่ ตัวอย่างเช่นโดยการกำหนด
n = 1 สำหรับแต่ละ n, และ c = 0 ชุดพลังงาน 1 + x + x 2 + … + x n + …. เป็นเรื่องง่ายที่จะสังเกตได้ว่าเมื่อ x ε (-1, 1) ชุดพลังงานนี้จะมาบรรจบกันเป็น 1 / (1-x)
= c. ค่าอื่น ๆ ที่ x ซึ่งชุดพลังงานสังวัตนาจะมีรูปแบบของช่วงเวลาเปิดอยู่กึ่งกลางที่ c นั่นคือ, จะมีค่า0≤ R ≤∞ เพื่อให้แต่ละ x เป็นที่น่าพอใจ | xc | ≤ R ซีรีส์พลังงานเป็นแบบรวมกันและสำหรับแต่ละ x ทำให้พอใจ | xc |> R ชุดพลังงานมีความแตกต่างกัน ค่านี้ R เรียกว่ารัศมีการบรรจบกันของชุดกำลัง (R สามารถใช้ค่าจริงหรือค่าอินฟินิตี้บวก)
ฉัน อี
ชุดเทย์เลอร์คืออะไร?
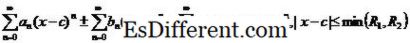
f (
x) ซึ่งมีความแตกต่างกันอย่างไม่มีที่สิ้นสุดในช่วงเวลา สมมติว่า f (x) จะแตกต่างกันในช่วงที่มีศูนย์กลางอยู่ที่ c. ชุดพลังงานที่ได้รับจาก
) ประมาณ 999 องศาเซลเซียส (ที่นี่ f (n) (c) หมายถึงอนุพันธ์ของ n th ที่ x = ค ) ในการวิเคราะห์เชิงตัวเลขจำนวนประโยคที่ จำกัด ในการขยายตัวที่ไม่มีขีด จำกัด นี้จะใช้ในการคำนวณค่าในจุดที่ชุดมีการบรรจบกับฟังก์ชันดั้งเดิม ฟังก์ชัน f (x) จะถูกวิเคราะห์ในช่วง (a, b) หากแต่ละ x ε (a, b) ชุดเทย์เลอร์ f (x) จะมาบรรจบกับฟังก์ชัน f (x) ยกตัวอย่างเช่น 1 / (1-x) เป็นตัววิเคราะห์ (-1, 1) ตั้งแต่การขยายเทย์เลอร์ 1 + x + x 2 + … + x n + … converges กับฟังก์ชันในช่วงนั้นและ x สามารถวิเคราะห์ได้ทุกที่ตั้งแต่ชุดเทย์เลอร์ e x converges ถึง e x < สำหรับแต่ละจำนวนจริง x อะไรคือข้อแตกต่างระหว่าง Power series และ Taylor series? 1 ชุดเทย์เลอร์เป็นชุดพิเศษของซีรีย์พลังงานที่กำหนดไว้สำหรับฟังก์ชั่นที่มีความแตกต่างกันอย่างไม่มีที่สิ้นสุดในบางช่วงเวลาที่เปิด 2 เทย์เลอร์ซีรีส์มีรูปแบบพิเศษ ในขณะที่ซีรี่ส์พลังงานสามารถเป็นได้ทุกรูปแบบ
